Radiative effects in gap opening by planets in protoplanetary disks
Alexandros Ziampras (Uni Tübingen), Wilhelm Kley (Uni Tübingen), Cornelis P. Dullemond (ITA, Heidelberg)
Click on text that looks like
this
Hi! This is a popup with additional information. I didn't want to stuff too much info on the poster itself, but let the reader control how much they would like to read. This both helps to avoid flooding experts with information they already know about, and to quickly bring people new to the subject up to speed. You can have multiple popups active at once, and you can close them away by clicking/tapping on them (or their source text)!
for more information! Or,
click here for a tl;dr
Relevant in: numerical modeling of planet formation, protoplanetary disks, dust-gas mechanics, planet-disk interaction.
What we did: We compared locally isothermal to radiative models of two popular systems that show prominent rings and gaps.
Why we did that: We want to test the planet formation scenario and at the same time verify whether radiative models show the same features as simpler, locally isothermal ones.
What we found: We found that the commonly used "locally isothermal" equation of state sometimes results in unexpected/unphysical results even when it seems justifiable. That's because it overestimates how quickly the planet's spiral arms can carry away angular momentum, which affects gap opening efficiency and spiral arm contrast.
.
The
DSHARP survey
Short for "Disk Substructures at High Angular Resolution Project", this survey featured observations of young stellar objects in an attempt to study the structures that can form in protoplanetary disks. (Link to page)
revealed a variety of substructures such as rings and gaps and opened possiblities to test the planet–disk interaction theory. These structure-rich systems show resolved features at the 50–100 au scale, where the disks are likely passive, optically thin, and starlight-heated. This suggests short
cooling timescales
In general, the cooling timescale $t_\text{cool}$ of a disk depends on properties such as its opacity and density, something that is self-consistently calculated in radiative models that account for viscous/irradiation heating and thermal cooling. Typically, $t_\text{cool}$ is expressed in units of the orbital timescale $\Omega_K^{-1}$, with $\beta=t_\text{cool}\Omega_\text{K}$. At the limit of $\beta\rightarrow 0$, the disk shows a fixed temperature profile and can be dubbed "locally isothermal". The disks observed by DSHARP seem to fulfill this requirement of cooling being much faster than the orbital timescale, due to the distances from the host star that ALMA can resolve reliably.
and makes modeling these systems with a
locally isothermal
By "locally isothermal" we refer to an equation of state where the disk temperature is prescribed and kept fixed, usually as a function of radius from the star. In contrast, an adiabatic equation of state accounts for the evolution of the thermal energy of the gas in time and models heating and cooling mechanisms in real time. A disk with a short cooling timescale typically shows no thermal evolution, and therefore an adiabatic EOS might be unnecessary at times.
equation of state reasonable. For AS 209, the gap structure of the resolved disk could be reconstructed with a single planet
exceptionally well
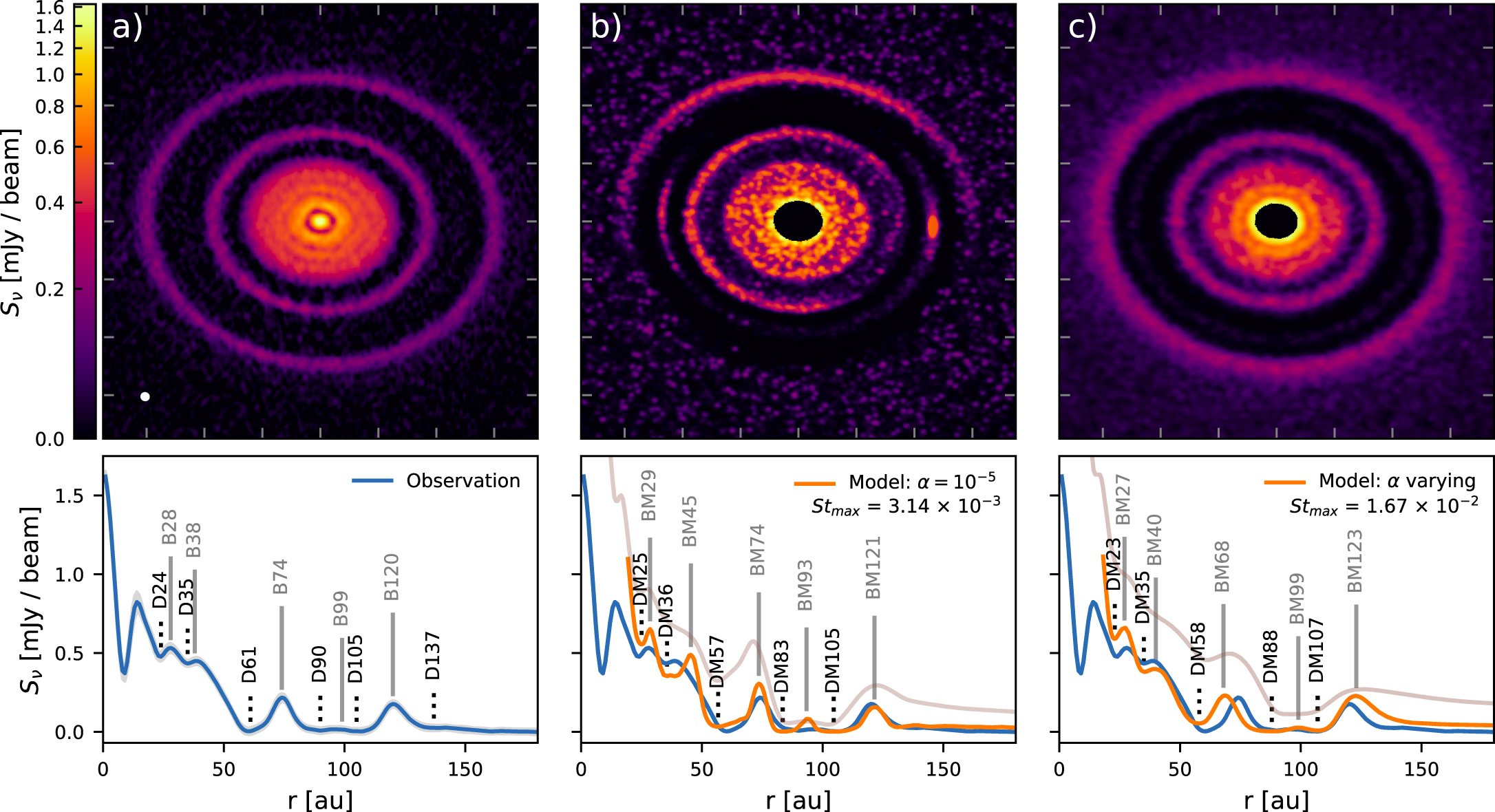 Zhang et. al (2018) show that based on a numerical model, a 0.1-Jupiter-mass planet in a locally isothermal disk could be responsible for 5 of the 6 resolved gaps (the 9 au gap was out of the simulation domain). (ADS)
assuming locally isothermal conditions.
Zhang et. al (2018) show that based on a numerical model, a 0.1-Jupiter-mass planet in a locally isothermal disk could be responsible for 5 of the 6 resolved gaps (the 9 au gap was out of the simulation domain). (ADS)
assuming locally isothermal conditions.
Motivation
Young planets inside a gaseous disk can interact gravitationally with the disk, launching spirals that carry angular momentum away from the planet. This mechanism can lead to
gap opening
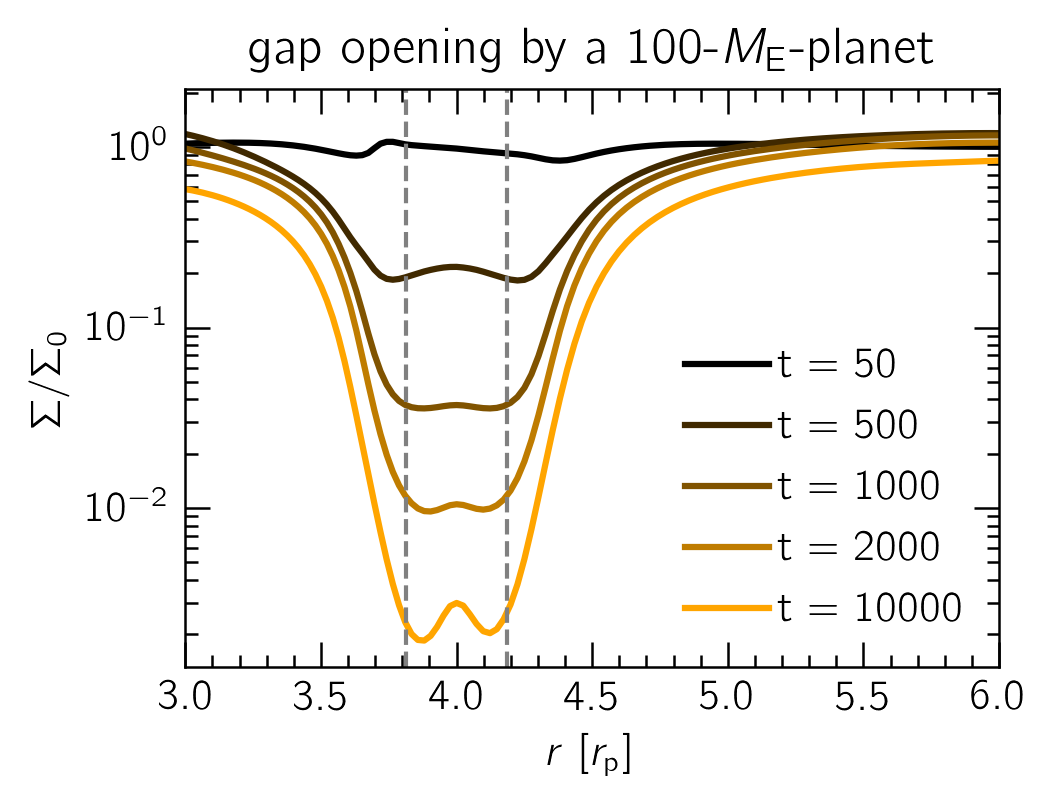
A gap will open as the spirals can transport angular momentum away from the planet. This is a lot easier for more massive planets or specific disk conditions. More info: Kley & Nelson (2012)
,
and the formation of bright
rings in continuum emission

The spirals can create pressure bumps, where dust particles can be trapped and collected. This usually leads to the formation of rings or crescents.
.
Miranda & Rafikov (2019) showed that, in disks with embedded planets, the angular momentum flux carried by spirals depends on the
cooling time per orbital period $\beta$
With $\beta$ we refer to the ratio of the cooling timescale $t_\text{cool}$ to the orbital timescale $\Omega_\text{K}^{-1}$, or $\beta=t_\text{cool}\Omega_K$. This fraction tends to zero or infinity for locally isothermal or adiabatic gas respectively.
such that a disk can be considered "locally isothermal" for $\beta < 10^{-3}\text{–}10^{-2}$ depending on planet mass.
At the same time, ALMA observations also suggest short cooling timescales around this range.
So the question is: How short is "short enough"?
We would like to examine the planet–disk interaction scenario if we are to attribute the observed ring/gap structures to young planets and understand the impact of the cooling timescale. To that end, we aim to test the locally isothermal assumption by modeling radiative effects such as heating and cooling and comparing the two equations of state to each other.
Model
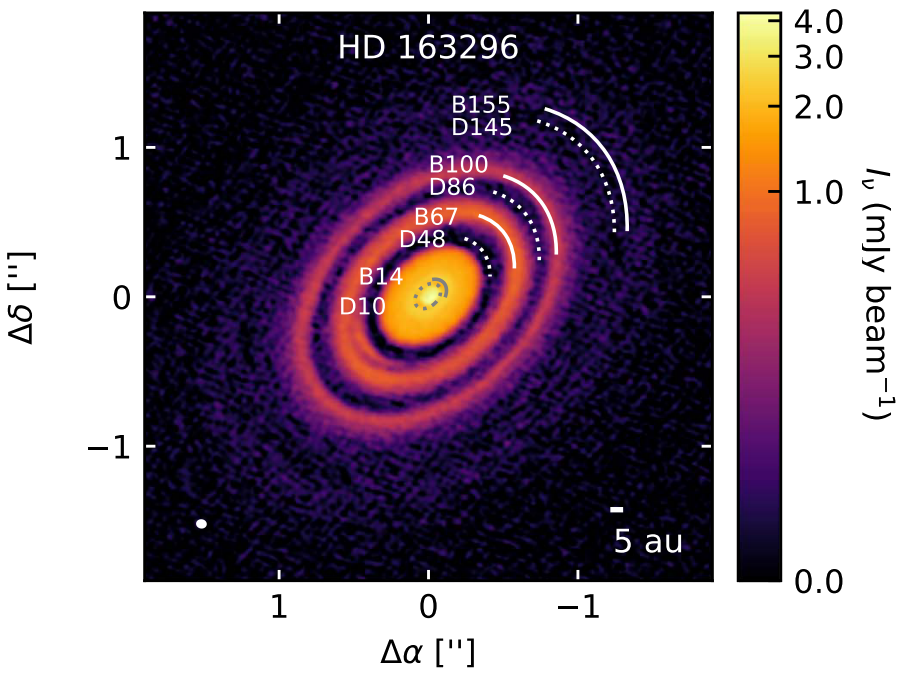
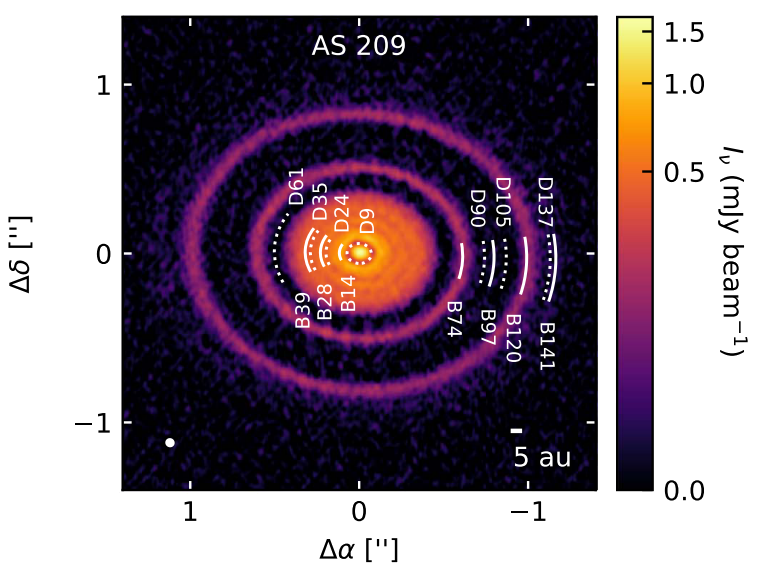
We model HD 163296 A 12.6-Myr-old, likely isolated, system that hosts a star with roughly $M_\ast\approx2.1\,M_\odot$ and $L_\ast\approx 17\,L_\odot$. The system features at least two clearly visible gaps at 48 and 86 au and two corresponding rings at 67 and 100 au. Image credit: Huang et al. (2018) and AS 209 A 1-Myr-old system in the Ophiuchus region that hosts a star with roughly $M_\ast\approx0.83\,M_\odot$ and $L_\ast\approx 1.4\,L_\odot$. The system is rich in annular structures, boasting five rings between 20–130 au. Image credit: Huang et al. (2018) with PLUTO A freely distributed 3D numerical hydrodynamics package featuring a Godunov-type Riemann solver to integrate conservation laws. The program was introduced by Mignone et al. (2007) and has been receiving continuous support since then. PLUTO homepage to reconstruct their ring/gap structures. We run both locally isothermal \[ \frac{\partial e}{\partial t} = 0\Rightarrow T(r) = T_0 r^{-q} \] By "locally isothermal" we refer to an equation of state where the disk temperature is prescribed and kept fixed, usually as a function of radius from the star. In contrast, an adiabatic equation of state accounts for the evolution of the thermal energy of the gas in time and models heating and cooling mechanisms in real time. and radiative \[ \frac{\partial e}{\partial t} + \nabla\cdot(e \vec{u}) = -p\nabla\cdot\vec{u} + Q_\text{visc} + Q_\text{irrad} - Q_\text{cool}\] Radiative models allow the temperature of the disk to evolve based on adiabatic effects, as well as additional heating and cooling from various sources. models with embedded planets, with initial profiles based on DSHARP. Our radiative models include a treatment for viscous\[ Q_\text{visc} = (\bar{σ}\cdot\nabla)\cdot \vec{u} \approx \frac{9}{4} \nu \Sigma \Omega_\text{K}^2,\qquad\nu = \alpha c_\text{s} H \] We assume an $\alpha$-viscosity model after Shakura & Sunyaev (1973), where turbulence is expressed as a small fraction of the gas pressure and prescribed as a viscous stress tensor $\bar{σ}$. To be able to compare to previous studies, we use an $\alpha$ of $10^{-4}$ and $10^{-5}$ for HD-163296 and AS-209, respectively. In our models, however, viscosity has little to no impact on the total heating. /shock\[ Q_\text{shock} = p\nabla\cdot\vec{u}\] The spiral waves launched by the embedded planets steepen into shocks, depositing heat into the disk through compression. This is taken into account by the numerical solver we are using, but adds very little heating compared to irradiation. /irradiation\[ Q_\text{irrad} = 2\frac{L_\ast}{4\pi r^2} (1-\epsilon) \left(\frac{\mathrm{d}\log H}{\mathrm{d}\log r} - 1 \right)\frac{h}{\tau_\text{eff}},\quad\epsilon=0.5,\quad\frac{\mathrm{d}\log H}{\mathrm{d}\log r} = \frac{9}{7} \] Heating through incident starlight is modeled according to a simple prescription by Menou & Goodman (2004), based on geometrical arguments and corrected for the disk opacity. Irradiation is the dominant heat source in our models. heating and thermal cooling\[ Q_\text{cool} = 2\sigma_\text{SB}\frac{T^4}{\tau_\text{eff}},\qquad\tau_\text{eff} = \frac{3\tau}{8} + \frac{\sqrt{3}}{4} + \frac{1}{4\tau},\quad\tau\propto\kappa_\text{R}\Sigma\] The gas is allowed to cool based on the vertically-averaged radiation flux that can escape from the surfaces of the disk, corrected for the disk opacity. Disk equilibrium is decided by a balance between irradiation heating and thermal cooling. .
Simulations (click on an image to enlarge!)
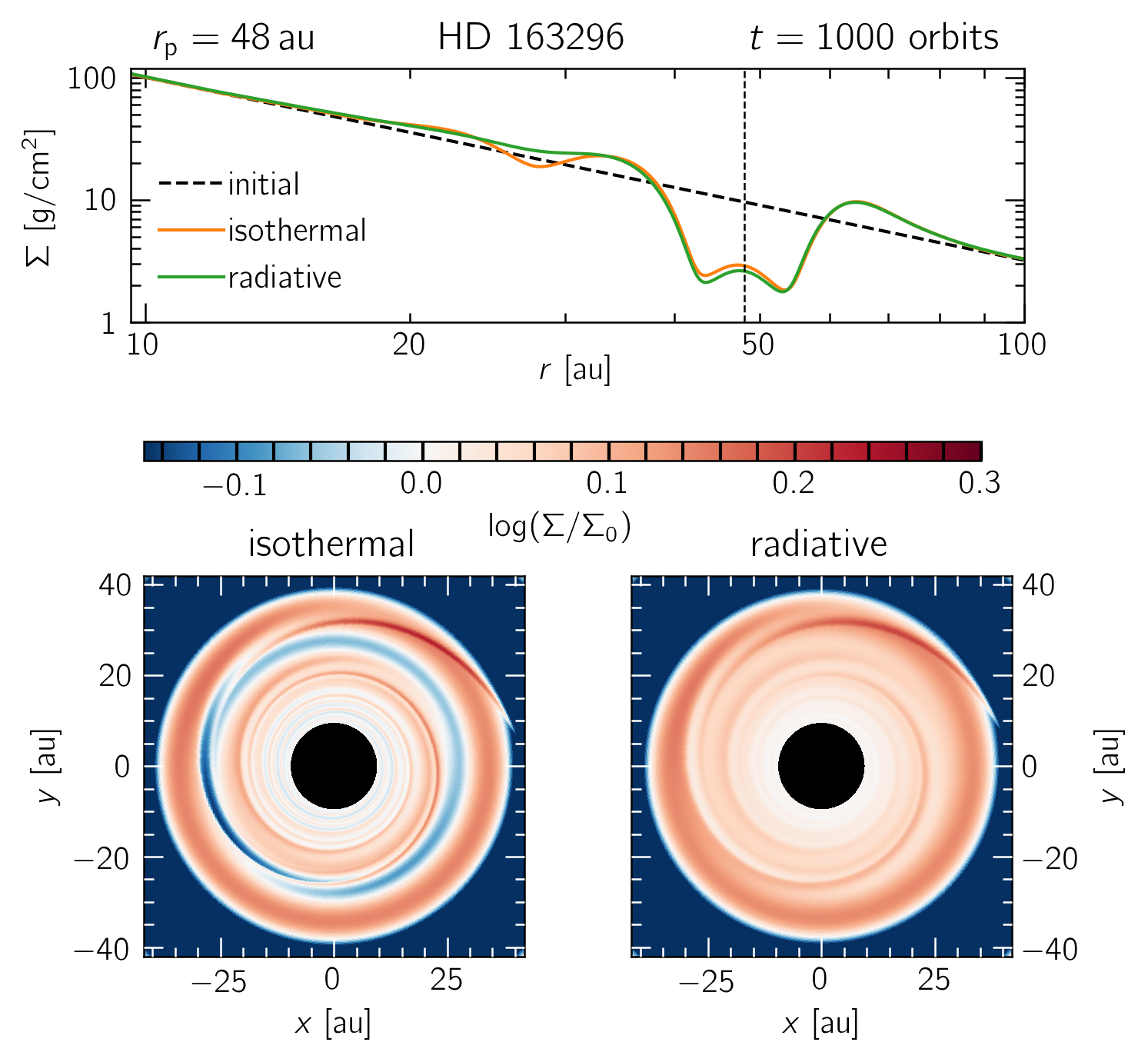
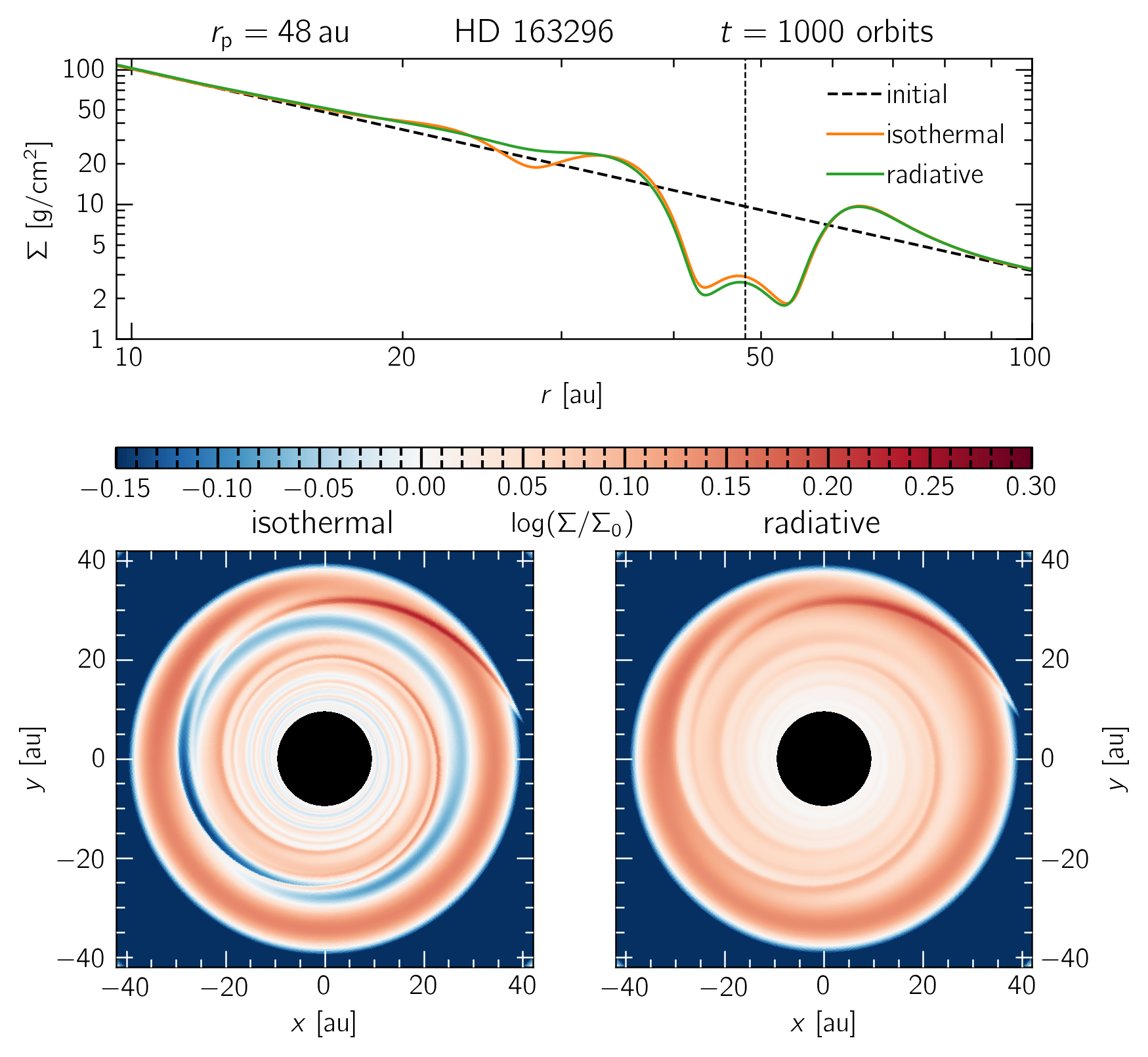
A comparison between locally isothermal and radiative disk models of HD 163296 with a single, $0.5 M_\text{J}$ planet at 48$\,$au. A secondary gap around 26 au and a stronger spiral arm contrast are evident in the locally isothermal model.
A comparison between locally isothermal and radiative disk models of HD 163296 with a single, $0.5 M_\text{J}$ planet at 48$\,$au. A secondary gap around 26 au and a stronger spiral arm contrast are evident in the locally isothermal model.
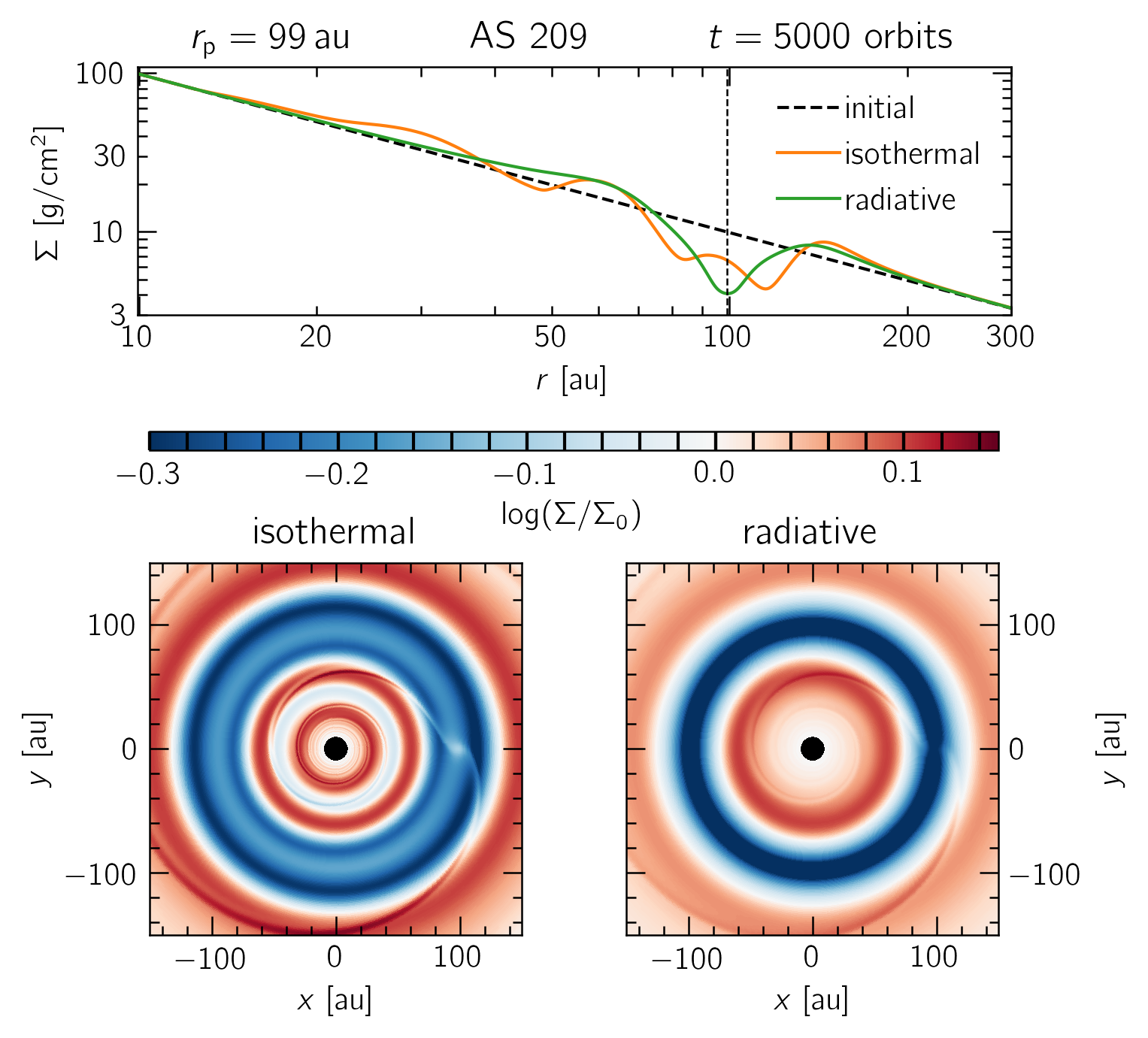
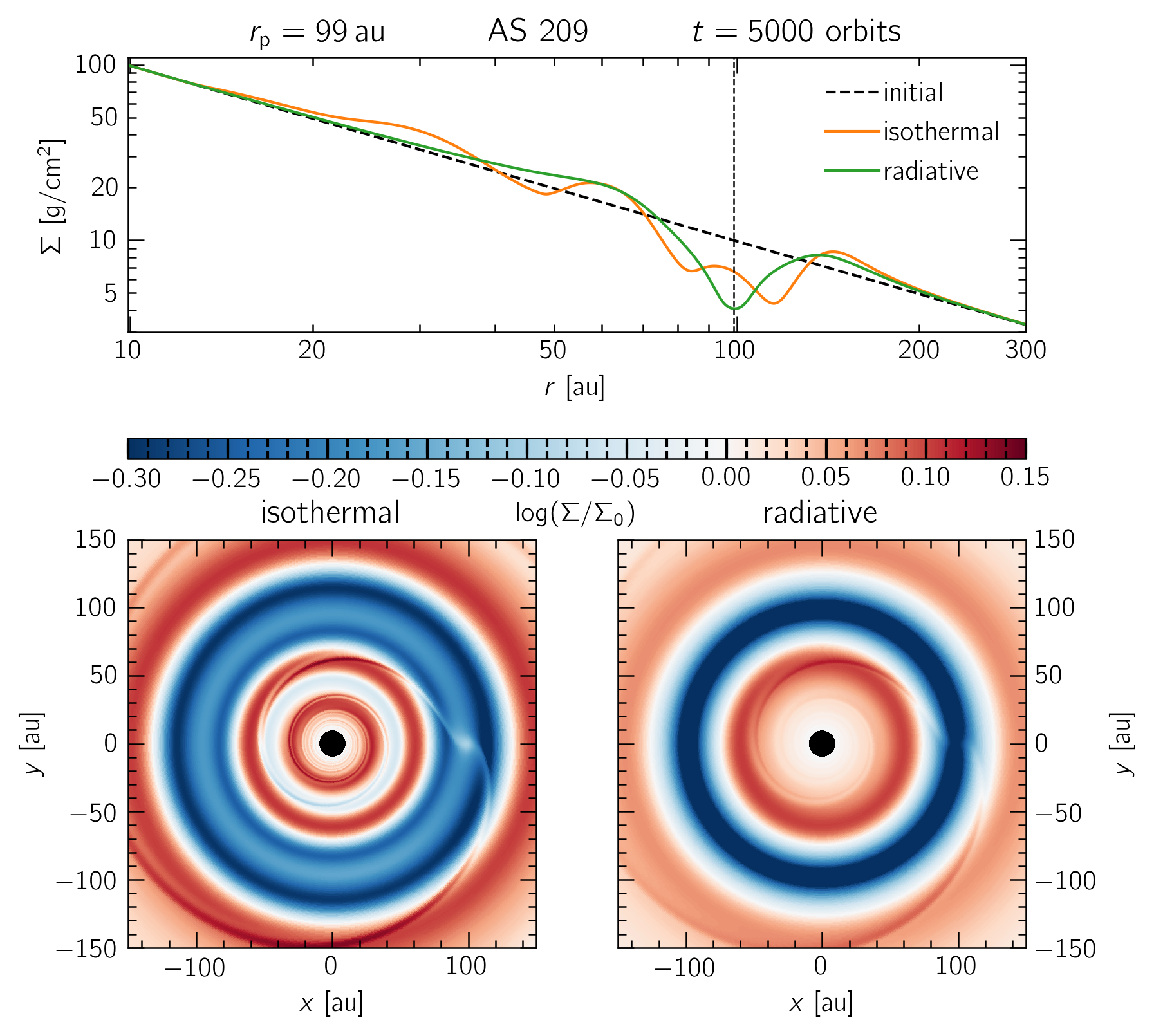
A comparison between locally isothermal and radiative disk models of AS 209 with a single, $0.1 M_\text{J}$ planet at 99$\,$au. A secondary gap is clearly visible around 50 au, and the primary gap structure is vastly different in the locally isothermal model.
A comparison between locally isothermal and radiative disk models of AS 209 with a single, $0.1 M_\text{J}$ planet at 99$\,$au. A secondary gap is clearly visible around 50 au, and the primary gap structure is vastly different in the locally isothermal model.
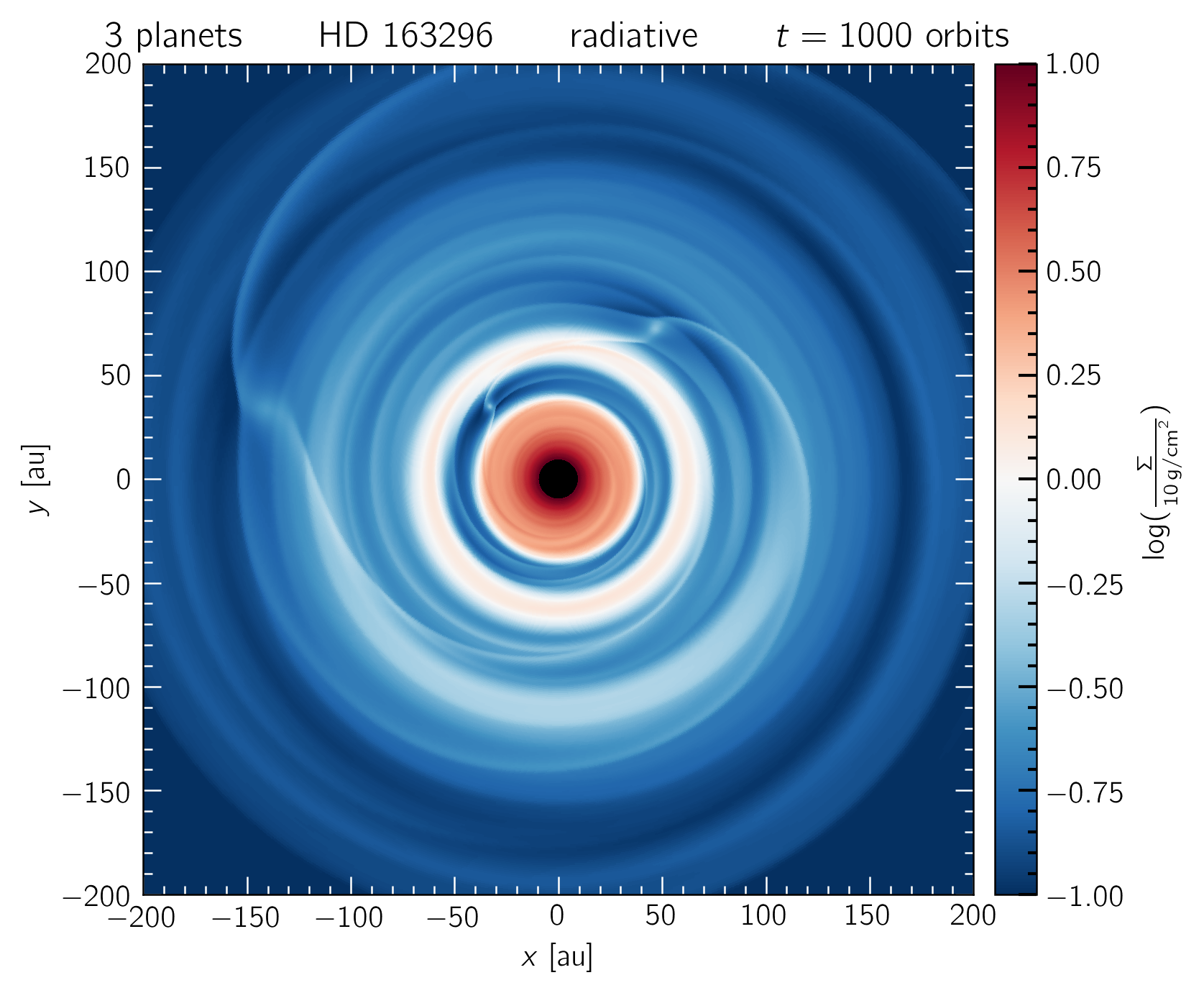
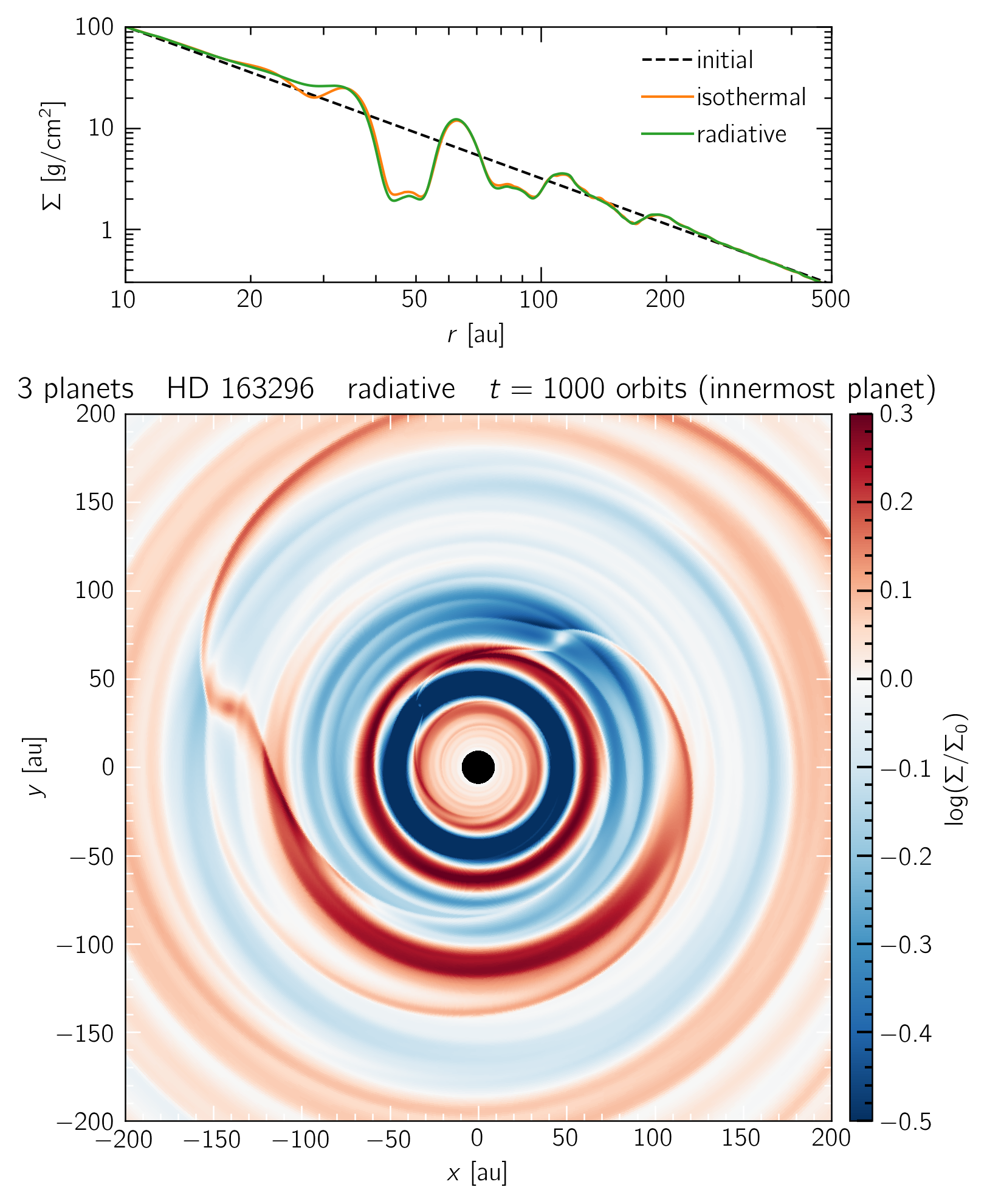
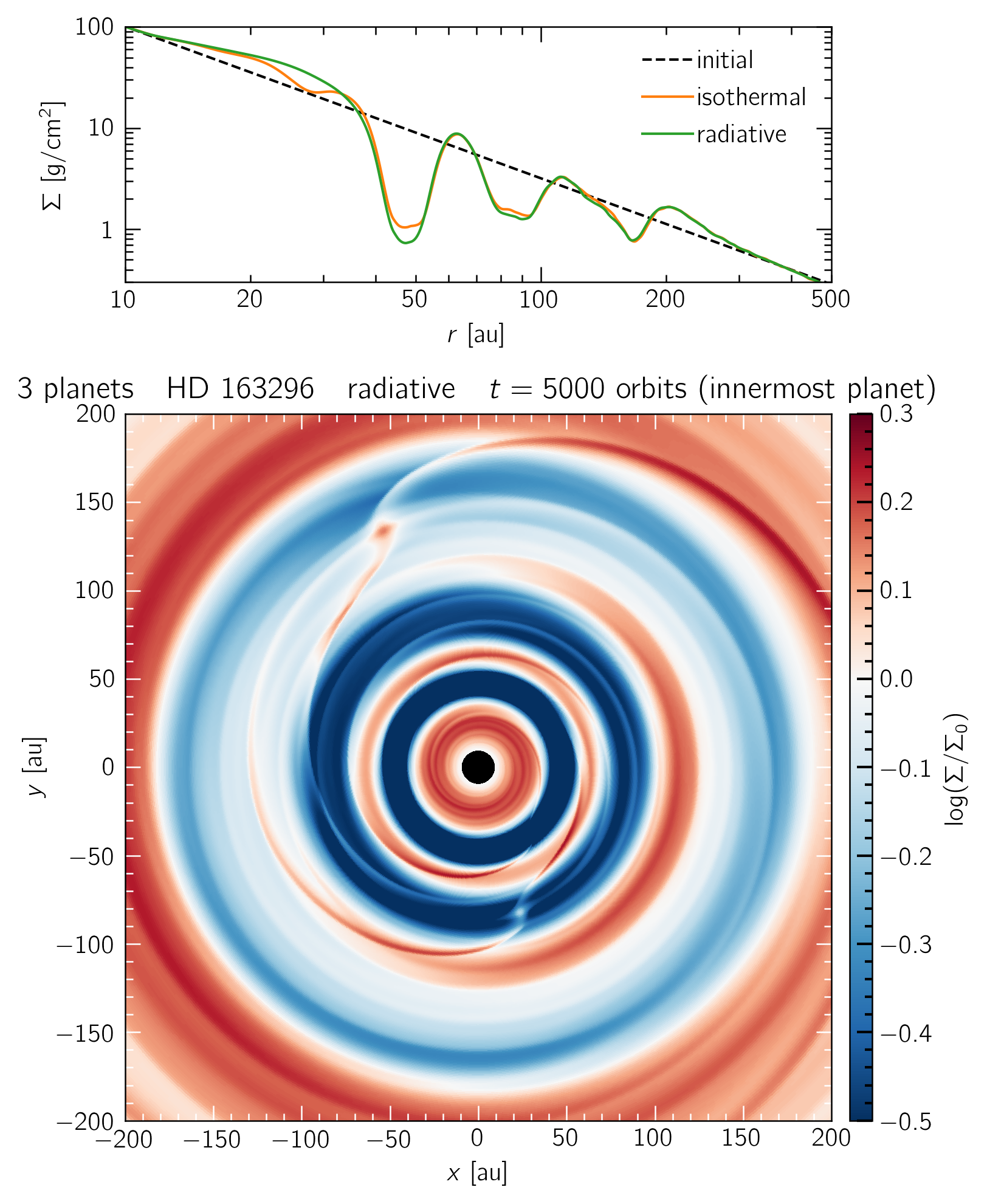
A radiative simulation of HD 163296 with 3 planets, embedded at radii where DSHARP detected a gap in continuum emission (48, 86, 145 au). The innermost 60 au show the same structure as our single-planet runs. The left and right panels show the disk state after 1000 and 5000 orbits of the innermost planet. The top panels show that the disk transitions to "truly" locally isothermal at large enough radii.
A radiative model of HD 163296 with 3 planets embedded at 48, 86 and 145 au. The innermost 60 au show the same structure as our single-planet runs.
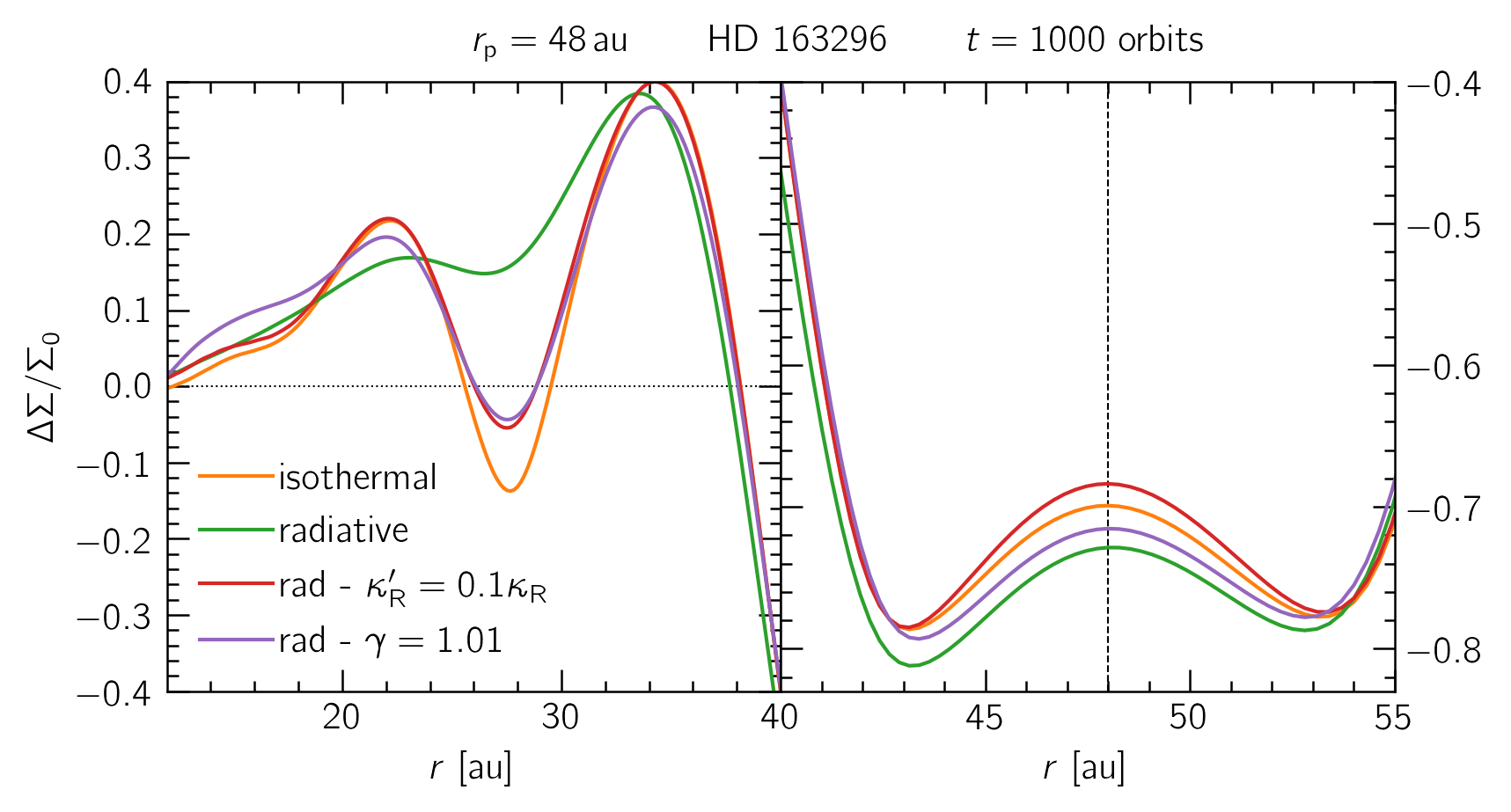

An attempt to reconstruct the locally isothermal limit by tweaking our parameters, such as increasing the efficiency of cooling by lowering the opacity or limiting adiabatic effects by bringing the adiabatic index close to unity. The tweaked models closely resemble the locally isothermal results, showing a weak density dip at around 28 au. For reference, the fiducial model has an opacity $\kappa_\text{R}$ = 0.45 cm²/g and a $\gamma$ = 1.4.
An attempt to reconstruct the locally isothermal limit by tweaking our parameters. The tweaked models closely resemble the locally isothermal results.
What's happening?
Even though the presence of the planet doesn't affect the disk's temperature profile, radiative effects can still impact the planet's gap opening capacity. That is because, while the short cooling timescale prevents shocks from heating up the disk, it's still long enough to affect the angular momentum flux of the planet's spirals. Incidentally, these two systems show a cooling timescale profile that hovers around the range suggested by Miranda & Rafikov in the inner 50 and 120 au for HD and AS, respectively. As a result, the two equations of state show different results at those regions!
Results
We find that locally isothermal models overestimate the angular momentum flux carried away by spirals, and therefore enhance planet-generated features with respect to radiative models:
- gaps are deeper for locally isothermal disks compared to radiative ones,
- a single planet can open multiple gaps within its orbit, and
- spirals have slightly higher contrast, enhancing pressure bumps.
All of the above points support dropping the locally isothermal assumption in favor of a parameterized cooling prescription By estimating the cooling timescale as a function of radius (or keeping it constant), it is easy to control the efficiency of cooling throughout the disk such that the temperature is relaxed to a pre-calculated equilibrium profile, for example corresponding to a viscously heated or an irradiated disk. A typical prescription would be "beta cooling", where the temperature is relaxed to an equilibrium profile $T_0$ at a fraction $\beta$ of the orbital timescale: \[ \frac{\mathrm{d}T}{\mathrm{d}t} = -\frac{T-T_0}{t_\text{cool}},\qquad t_\text{cool} = \beta\Omega_\text{K}^{-1} \] or a self-consistent model of gas cooling An example would be a prescription of thermal cooling, or a more complex radiative transfer model. .
Conclusion
In general, the locally isothermal assumption proves to be dangerous even at the range of tens of au regarding planet–disk interaction and should therefore be avoided in favor of an adiabatic equation of state with a prescription for radiative cooling in the disk. The results between different equations of state converge in the limit of very short cooling timescales (0.1%-1% of the orbital timescale depending on planet mass), in good agreement with Miranda & Rafikov (2019).
Our results are consistent with previous studies and imply that a single planet cannot always explain the existence of multiple gaps. With that in mind, different possibilities can be explored to explain the origin of multiple gaps in the systems observed by ALMA.
References
ALMA Partnership (2018). ADS, DSHARP data
Zhang, S., et al. ApJ, 869, L47 (2018). ADS
Miranda, R. & Rafikov, R. R., ApJ, 878, L9 (2019). ADS
Miranda, R. & Rafikov, R. R., ApJ, 892, 1 (2020). ADS
More info
Our paper on this!
Model details: physics and numericsOur values for $\Sigma_0$ and $M_\text{p}$ are inspired from DSHARP. LP85 refers to the Lin & Papaloizou (1985) opacity table.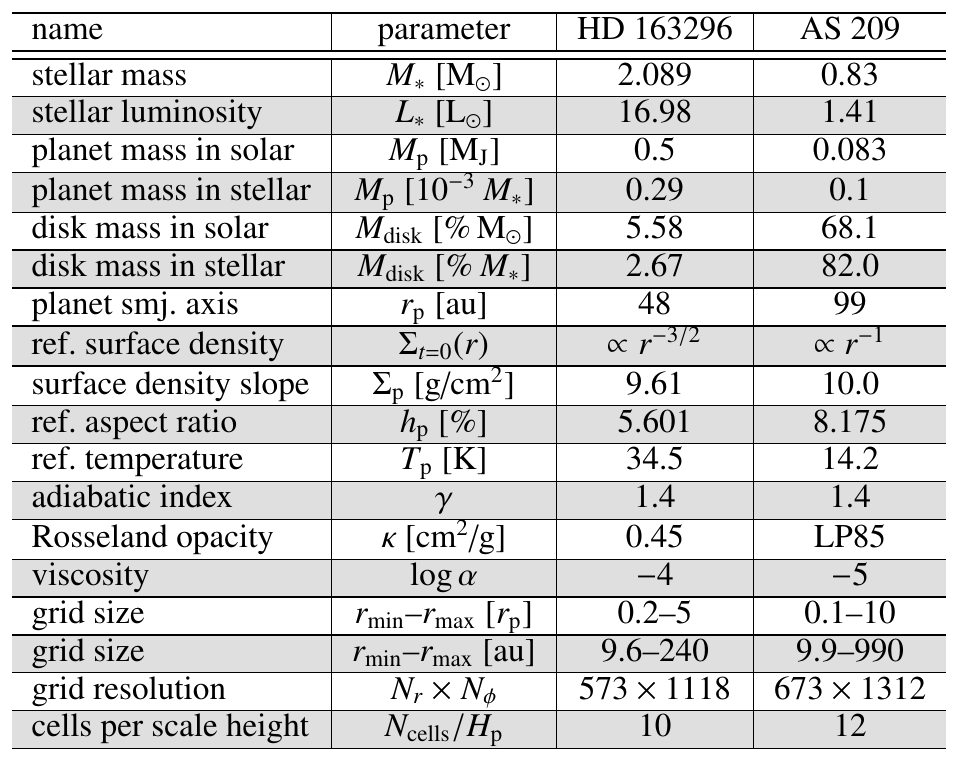
Model details: contribution of shock heating
As shown here, the heating by the planet's spirals results in temperature differences of the order of a few %. Irradiation really is the dominant source of heating, and the disk temperature profile barely changes with respect to the initial equilibrium state.
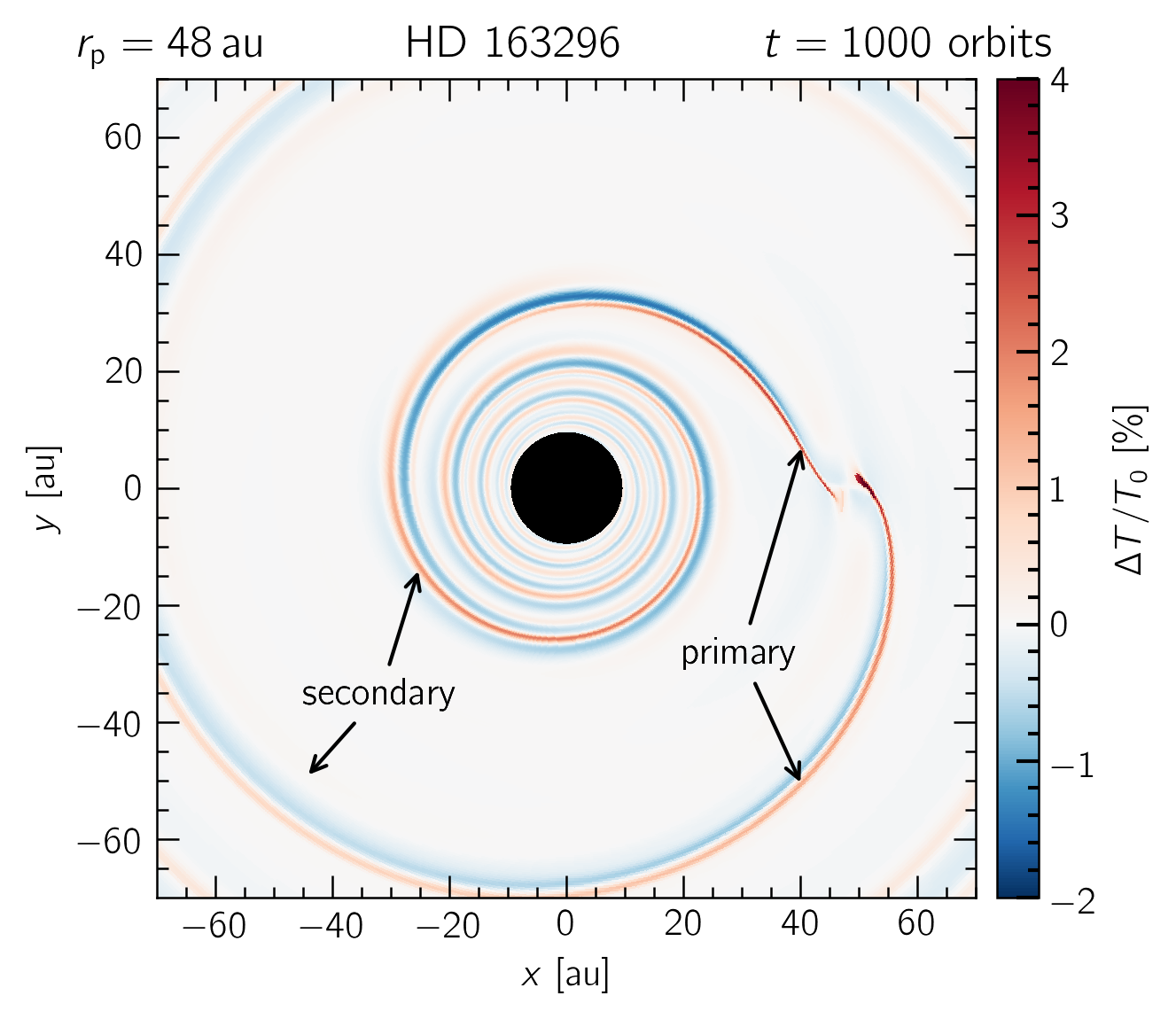
Results details: spiral arms
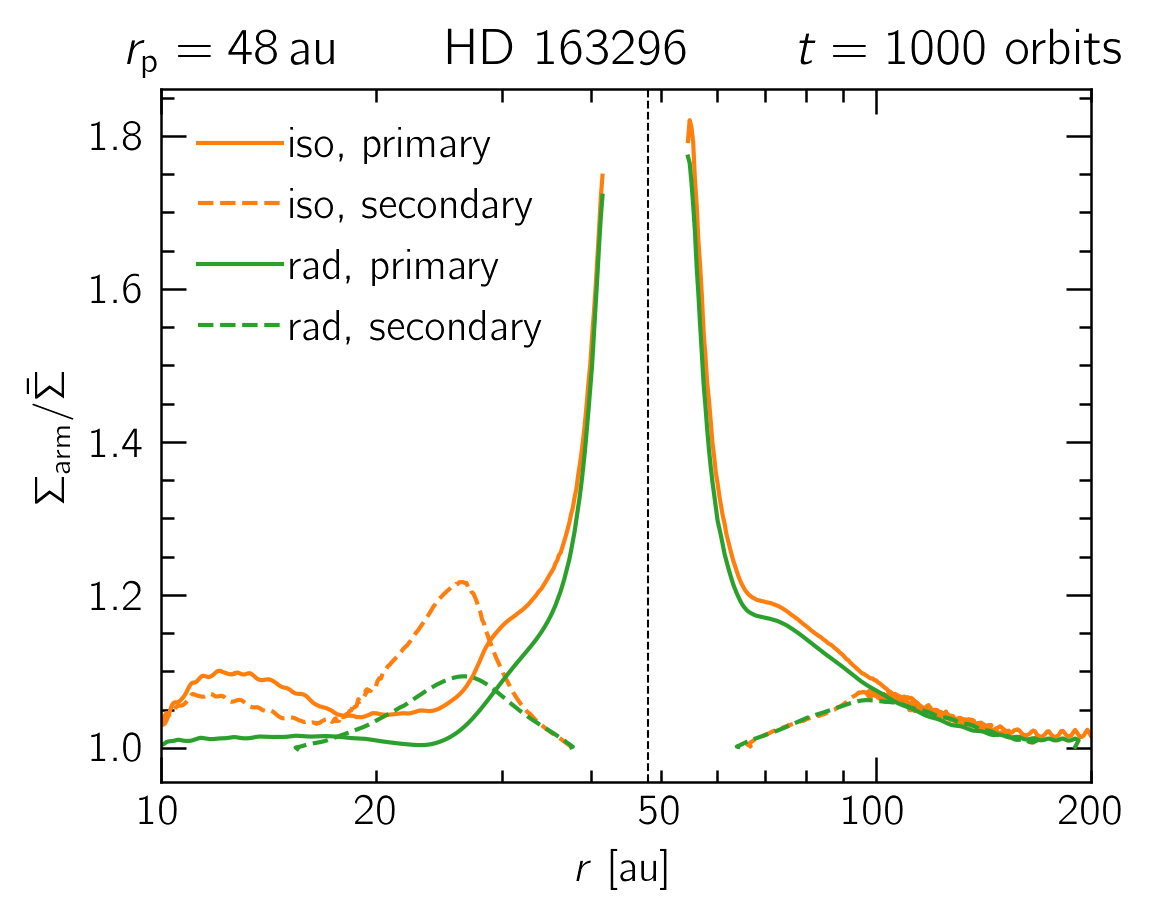
We can track individual spirals and monitor their contrast to the background flow. We found that this contrast can be significantly higher for locally isothermal models.
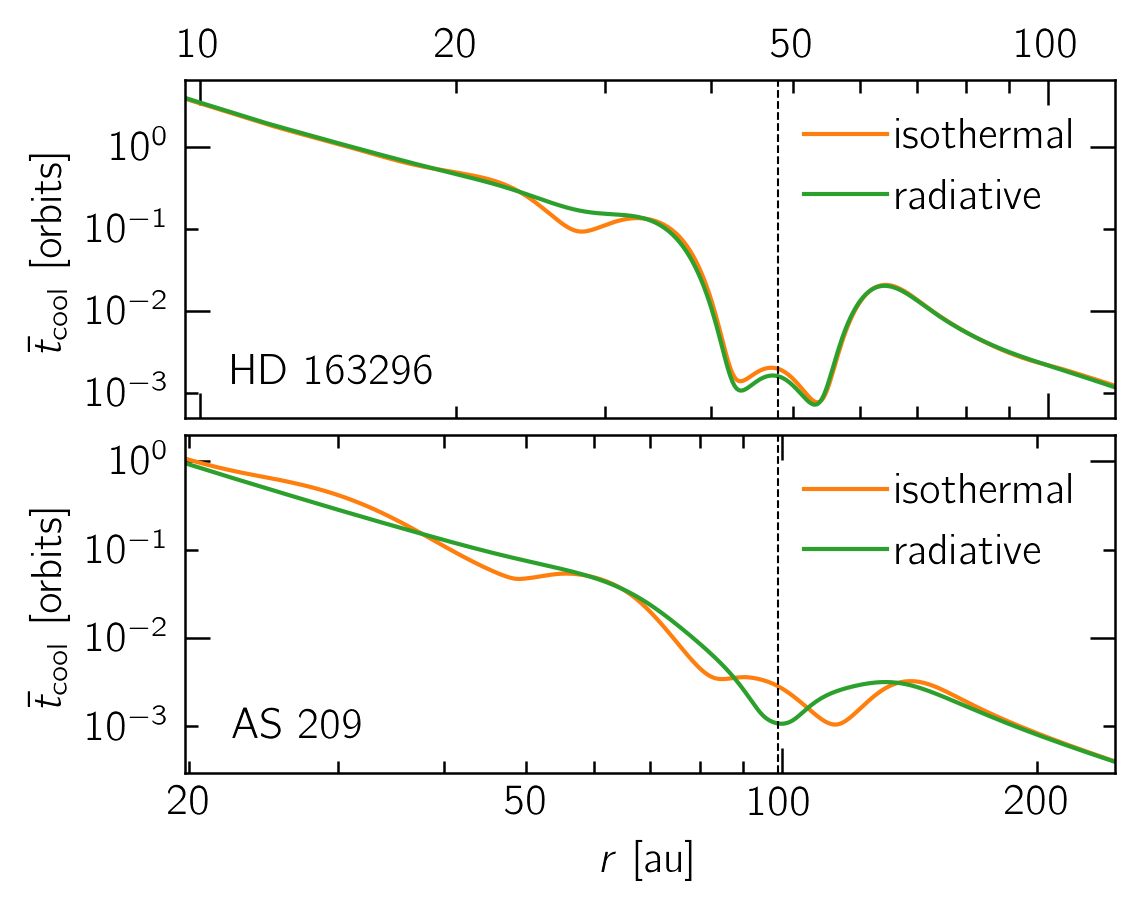
Extra details: an estimate of the cooling timescale
We can estimate the cooling timescale $t_\text{cool}$ by writing:
\[t_\text{cool} \sim \frac{e}{\dot{e}} \sim \frac{e}{Q_\text{cool}},\quad Q_\text{cool} \propto \frac{T^4}{\kappa_\text{R}\Sigma}\Rightarrow t_\text{cool}\propto\frac{\kappa_\text{R}\Sigma^2}{T^3},\]
Which we can then plot to get an idea of how important radiative effects would be. As expected, we find that the $t_\text{cool}$ is not short enough to be ignored.
The fine print
Of course, these results should be taken with a grain of salt for several reasons. Most importantly, the error bars on the estimates for the gas surface density or the dust opacity in the observed disks are large enough to sometimes cover orders of magnitude. Additional physics could also come into play: dust-gas interaction could possibly interfere, leading to the formation of vortices that could disrupt the image we constructed, while dust growth could significantly reduce the opacity, lowering the cooling timescale. At the same time, non-ideal MHD effects or self-gravity could certainly come into play given the distance of our targets from the star and the estimates for the mass of some of the disks.


